篇首语：本文由编程笔记#小编为大家整理，主要介绍了MAML小样本学习算法解读及基于飞桨的代码实现相关的知识，希望对你有一定的参考价值。
研究背景及基本概念
研究背景
深度学习之所以在近年来大获成功&＃xff0c;很大程度上得益于大数据技术的发展。深度神经网络强大的函数拟合能力&＃xff0c;需要通过在人工标注的大数据集上长时间训练&＃xff0c;才能获得强泛化能力&＃xff0c;从而应用于各行各业。相比深度学习模型&＃xff0c;人类智能只需要通过少量几张图片&＃xff0c;就能迅速准确地学习掌握图像中类别主体的关键本质特征&＃xff0c;并推广到同类别其他从未见过的样本上。如何使深度神经网络模拟人类学习的过程&＃xff0c;高效地训练&＃xff0c;习得新概念&＃xff0c;是深度学习下一步要攻克的重要难题。小样本学习&＃xff08;Few-Shot Learning&＃xff0c;FSL&＃xff09;的相关研究&＃xff0c;即是实现该目标的重要环节。
MAML元学习算法是小样本学习领域中的经典方法&＃xff0c;本文将重点讲解该方法的理论和飞桨代码实现。本章首先对小样本学习的问题定义、评价标准和常用数据集进行介绍&＃xff0c;以期读者对本领域概况获得基本了解。
问题定义
假设数据集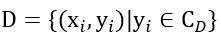
中包含 个类别&＃xff0c;将这个数据集按类别划分为不相交的两部分&＃xff0c;一部分称为基础集&＃xff08;Base set&＃xff09;
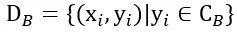&＃xff0c;一部分称为新颖集&＃xff08;Novel Set&＃xff09;
&＃xff0c;其中&＃xff0c; &＃xff0c;且 。模型在基础集上离线训练&＃xff0c;以获得所需的先验知识和特征提取能力。在基础集上的具体训练方式&＃xff0c;因算法的不同而异。对新颖集 随机采样N个类别&＃xff0c;每个类别采样K个样本&＃xff0c;这 个带标签的样本构成支持集&＃xff08;Support set&＃xff09;S&＃xff0c;小样本学习任务便是在这个很小的数据集S上进行&＃xff0c;称为N-way K-shot任务。此外&＃xff0c;对这N个类别再采样 个无标签样本构成查询集Q&＃xff0c;在Q上进行小样本模型的分类测试。通常&＃xff0c;N&＃61;5&＃xff0c;K&＃61;1或5。
本文所述的MAML算法&＃xff0c;是在基础集上以相同方式构建了若干个N-way K-shot训练任务&＃xff0c;进行离线训练。这种训练方式是一种元学习的训练方法&＃xff0c;保持了与测试过程相同的任务构建流程&＃xff0c;能够最大程度避免协变量偏移。
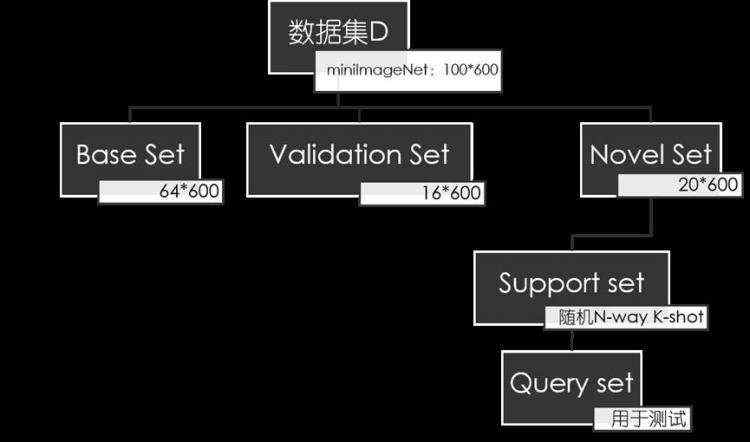
为了更清晰地展示数据集的划分方法&＃xff0c;这里以miniImageNet数据集[1]为例&＃xff0c;进行图形化展示&＃xff0c;如下图所示。该数据集共有100个类别&＃xff0c;每个类别各有600张图像样本。
评价标准
在600轮&＃xff08;或1000轮等等&＃xff09;不同的N-way K-shot任务上&＃xff0c;分别进行小样本学习&＃xff0c;得到在查询集上的top-1分类准确率。最终的评估指标是这600个任务上的平均准确率和置信区间。
常用数据集
miniImageNet[1]&＃xff1a;由Oriol Vinyals等在Matching Networks[1]中首次提出。在Matching Networks中&＃xff0c; 作者提出对ILSVRC-12中的类别和样本进行抽取&＃xff08;参见其Appendix B&＃xff09;&＃xff0c;形成了一个数据子集&＃xff0c;将其命名为miniImageNet&＃xff0c;包含100类共60000张彩色图片&＃xff0c;其中每类有600个样本&＃xff0c;图像大小为84×84。随后&＃xff0c;普林斯顿大学的博士生Sachin Ravi[2]将该数据集随机划分为64个基础集类&＃xff0c;16个验证集类和20个新颖集类。
下载链接&＃xff1a;
https://aistudio.baidu.com/aistudio/datasetdetail/105646
tieredImageNet[3]&＃xff1a;同样是ILSVRC-12的子集&＃xff0c;包含ImageNet中层次结构较高级别的34个大类&＃xff08;category&＃xff09;&＃xff0c;每个大类包含10~30个小类&＃xff08;class&＃xff09;。该数据集中各子集的划分方法如下表所示。
下载链接&＃xff1a;
https://aistudio.baidu.com/aistudio/datasetdetail/92380
FC100[4]&＃xff1a;即Fewshot-CIFAR100&＃xff0c;截取自CIFAR100数据集&＃xff0c;共包含100个类别&＃xff0c;每个类别600张图片&＃xff0c;图像大小为32×32×3。其中基础集60个类别&＃xff0c;验证集和新颖集各60个类别。
下载链接&＃xff1a;
https://aistudio.baidu.com/aistudio/datasetdetail/92333
Omniglot[5]&＃xff1a;包含50个不同的字母表&＃xff0c;每个字母表中的字母各包含20个手写字符样本&＃xff0c;每一个手写样本都是不同人通过亚马逊Mechanical Turk在线绘制的。Omniglot数据集的多样性强于MNIST数据集&＃xff0c;常用于小样本识别任务。
下载链接&＃xff1a;
https://aistudio.baidu.com/aistudio/datasetdetail/78550
CUB[6]&＃xff1a;该数据集是一个细粒度数据集&＃xff0c;全部由鸟类图片构成&＃xff0c;共包含200个类别&＃xff0c;其中100个类别为基础集&＃xff0c;50个类别为验证集&＃xff0c;50个类别为新颖集。
下载链接&＃xff1a;
https://aistudio.baidu.com/aistudio/datasetdetail/23613
MAML模型算法
模型无关元学习&＃xff08;Model-Agnostic Meta-Learning&＃xff0c;简称MAML&＃xff09;算法[7]&＃xff0c;其模型无关体现在&＃xff0c;能够与任何使用了梯度下降法的模型相兼容&＃xff0c;广泛应用于各种不同的机器学习任务&＃xff0c;包括图像分类、目标检测、强化学习等。元学习的目标&＃xff0c;是在大量不同的任务上训练一个模型&＃xff0c;使其能够使用极少量的训练数据&＃xff08;即小样本&＃xff09;&＃xff0c;进行极少量的梯度下降步数&＃xff0c;就能够迅速适应新任务&＃xff0c;解决新问题。
模型方法
MAML算法的训练目的是获得一组最优的初始化参数&＃xff0c;使得模型能够快速适配&＃xff08;fast adaptation&＃xff09;新任务。作者认为&＃xff0c;某些特征比另一些特征更容易迁移到其他任务中&＃xff0c;这些特征具有跨任务间的通用性。既然小样本学习任务只提供少量标记样本&＃xff0c;模型在小样本上多轮迭代训练后必然导致过拟合&＃xff0c;那么就应该尽可能使模型只迭代训练几步。这就要求模型已经具有广泛适配于各种任务的初始化参数&＃xff0c;这组参数应包含模型在基础集上所学到的先验知识。
假设模型可以用函数 θ 表示&＃xff0c;θ为模型参数。适配新任务 时&＃xff0c;模型通过梯度下降法迭代一步&＃xff08;或若干步&＃xff09;&＃xff0c;参数θ更新为θ &＃xff0c;即 θθαθ
其中&＃xff0c; α为超参数&＃xff0c;用于控制适配过程的学习率。
在多个不同任务 上&＃xff0c;模型通过计算 θ 的损失来评估模型参数 θ 。具体地&＃xff0c;元学习的目标是获得一组参数 θ &＃xff0c;使得模型在任务分布 上&＃xff0c;能够快速适配所有任务&＃xff0c;使得损失最小。用公式表达如下&＃xff1a;
通过随机梯度下降&＃xff08;SGD&＃xff09;法&＃xff0c;模型参数 θ 按照以下公式进行更新&＃xff1a;
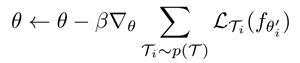
这里需要注意&＃xff0c;我们最终要优化的参数是 θ &＃xff0c;但计算损失函数却是在微调后的参数 θ 上进行&＃xff0c;训练过程可通过下图示意。
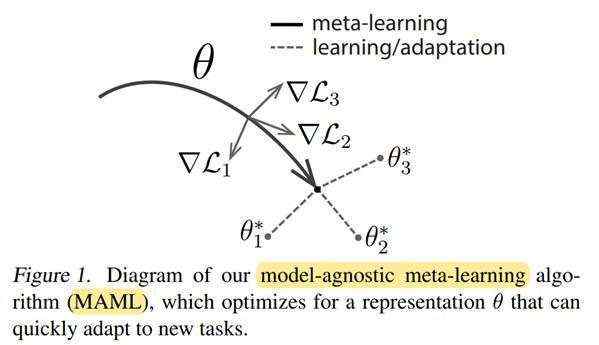
由于上述元学习算法在损失计算和优化参数方面的特点&＃xff0c;训练包括了两层循环。外层循环是元学习过程&＃xff0c;通过在任务分布
上采样一组任务
&＃xff0c;计算在这组任务上的损失函数&＃xff1b;内层循环是微调过程&＃xff0c;即针对每一个任务
&＃xff0c;迭代一次&＃xff08;或若干次&＃xff09;梯度下降&＃xff0c;将参数进行更新为 θ &＃xff0c;然后计算在参数为 θ 时的损失。梯度反向传递时&＃xff0c;需要跨越两层循环传递到初始参数θ上&＃xff0c;完成元学习的参数更新。
完整的MAML算法如下图所示。
实验结果
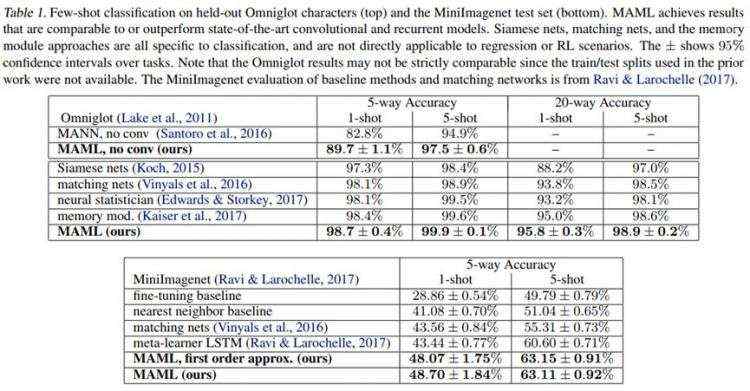
在Omniglot和miniImageNet数据集上&＃xff0c;文献给出的实验结果如下图所示。
飞桨实现
本小节给出本人在“飞桨论文复现挑战赛&＃xff08;第三期&＃xff09;”中完成的部分关键代码。完整项目代码已在GitHub和AI Studio上开源&＃xff0c;欢迎读者star、fork。链接如下&＃xff1a;
GitHub地址&＃xff1a;
https://github.com/hrdwsong/maml-paddle
AI Studio地址&＃xff1a;
https://aistudio.baidu.com/aistudio/projectdetail/1869590?contributionType&＃61;1&shared&＃61;1
关键代码实现
该模型比较特殊&＃xff0c;梯度需要穿过内外两层循环传递到原始参数。如果基于nn.Layer类进行常规的模型搭建&＃xff0c;在内循环更新梯度时&＃xff0c;模型参数会被覆盖&＃xff0c;导致初始参数丢失。得益于飞桨动态图模式灵活组网的特点&＃xff0c;本项目将模型参数和算子分离设计&＃xff0c;在外循环中保存原始参数副本 θ &＃xff1b;内循环中通过该副本更新参数&＃xff0c;计算损失函数。计算图通过动态图模式自动构建&＃xff0c;最终将梯度反传回原始参数 θ 。
MAML类的代码如下&＃xff1a;
1class MAML(paddle.nn.Layer):
2 def __init__(self, n_way):
3 super(MAML, self).__init__()
4 # 定义模型中全部待优化参数
5 self.vars &＃61; []
6 self.vars_bn &＃61; []
7 # ------------------------第1个conv2d-------------------------
8 weight &＃61; paddle.static.create_parameter(shape&＃61;[64, 1, 3, 3],
9 dtype&＃61;&＃39;float32&＃39;,
10 default_initializer&＃61;nn.initializer.KaimingNormal(),
11 is_bias&＃61;False)
12 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
13 dtype&＃61;&＃39;float32&＃39;,
14 is_bias&＃61;True) # 初始化为零
15 self.vars.extend([weight, bias])
16 # 第1个BatchNorm
17 weight &＃61; paddle.static.create_parameter(shape&＃61;[64],
18 dtype&＃61;&＃39;float32&＃39;,
19 default_initializer&＃61;nn.initializer.Constant(value&＃61;1),
20 is_bias&＃61;False)
21 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
22 dtype&＃61;&＃39;float32&＃39;,
23 is_bias&＃61;True) # 初始化为零
24 self.vars.extend([weight, bias])
25 running_mean &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
26 running_var &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
27 self.vars_bn.extend([running_mean, running_var])
28 # ------------------------第2个conv2d------------------------
29 weight &＃61; paddle.static.create_parameter(shape&＃61;[64, 64, 3, 3],
30 dtype&＃61;&＃39;float32&＃39;,
31 default_initializer&＃61;nn.initializer.KaimingNormal(),
32 is_bias&＃61;False)
33 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
34 dtype&＃61;&＃39;float32&＃39;,
35 is_bias&＃61;True)
36 self.vars.extend([weight, bias])
37 # 第2个BatchNorm
38 weight &＃61; paddle.static.create_parameter(shape&＃61;[64],
39 dtype&＃61;&＃39;float32&＃39;,
40 default_initializer&＃61;nn.initializer.Constant(value&＃61;1),
41 is_bias&＃61;False)
42 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
43 dtype&＃61;&＃39;float32&＃39;,
44 is_bias&＃61;True) # 初始化为零
45 self.vars.extend([weight, bias])
46 running_mean &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
47 running_var &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
48 self.vars_bn.extend([running_mean, running_var])
49 # ------------------------第3个conv2d------------------------
50 weight &＃61; paddle.static.create_parameter(shape&＃61;[64, 64, 3, 3],
51 dtype&＃61;&＃39;float32&＃39;,
52 default_initializer&＃61;nn.initializer.KaimingNormal(),
53 is_bias&＃61;False)
54 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
55 dtype&＃61;&＃39;float32&＃39;,
56 is_bias&＃61;True)
57 self.vars.extend([weight, bias])
58 # 第3个BatchNorm
59 weight &＃61; paddle.static.create_parameter(shape&＃61;[64],
60 dtype&＃61;&＃39;float32&＃39;,
61 default_initializer&＃61;nn.initializer.Constant(value&＃61;1),
62 is_bias&＃61;False)
63 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
64 dtype&＃61;&＃39;float32&＃39;,
65 is_bias&＃61;True) # 初始化为零
66 self.vars.extend([weight, bias])
67 running_mean &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
68 running_var &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
69 self.vars_bn.extend([running_mean, running_var])
70 # ------------------------第4个conv2d------------------------
71 weight &＃61; paddle.static.create_parameter(shape&＃61;[64, 64, 3, 3],
72 dtype&＃61;&＃39;float32&＃39;,
73 default_initializer&＃61;nn.initializer.KaimingNormal(),
74 is_bias&＃61;False)
75 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
76 dtype&＃61;&＃39;float32&＃39;,
77 is_bias&＃61;True)
78 self.vars.extend([weight, bias])
79 # 第4个BatchNorm
80 weight &＃61; paddle.static.create_parameter(shape&＃61;[64],
81 dtype&＃61;&＃39;float32&＃39;,
82 default_initializer&＃61;nn.initializer.Constant(value&＃61;1),
83 is_bias&＃61;False)
84 bias &＃61; paddle.static.create_parameter(shape&＃61;[64],
85 dtype&＃61;&＃39;float32&＃39;,
86 is_bias&＃61;True) # 初始化为零
87 self.vars.extend([weight, bias])
88 running_mean &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
89 running_var &＃61; paddle.to_tensor(np.zeros([64], np.float32), stop_gradient&＃61;True)
90 self.vars_bn.extend([running_mean, running_var])
91 # ------------------------全连接层------------------------
92 weight &＃61; paddle.static.create_parameter(shape&＃61;[64, n_way],
93 dtype&＃61;&＃39;float32&＃39;,
94 default_initializer&＃61;nn.initializer.XavierNormal(),
95 is_bias&＃61;False)
96 bias &＃61; paddle.static.create_parameter(shape&＃61;[n_way],
97 dtype&＃61;&＃39;float32&＃39;,
98 is_bias&＃61;True)
99 self.vars.extend([weight, bias])
100
101 def forward(self, x, params&＃61;None, bn_training&＃61;True):
102 if params is None:
103 params &＃61; self.vars
104 weight, bias &＃61; params[0], params[1] # 第1个CONV层
105 x &＃61; F.conv2d(x, weight, bias, stride&＃61;1, padding&＃61;1)
106 weight, bias &＃61; params[2], params[3] # 第1个BN层
107 running_mean, running_var &＃61; self.vars_bn[0], self.vars_bn[1]
108 x &＃61; F.batch_norm(x, running_mean, running_var, weight&＃61;weight, bias&＃61;bias, training&＃61;bn_training)
109 x &＃61; F.relu(x) # 第1个relu
110 x &＃61; F.max_pool2d(x, kernel_size&＃61;2) # 第1个MAX_POOL层
111 weight, bias &＃61; params[4], params[5] # 第2个CONV层
112 x &＃61; F.conv2d(x, weight, bias, stride&＃61;1, padding&＃61;1)
113 weight, bias &＃61; params[6], params[7] # 第2个BN层
114 running_mean, running_var &＃61; self.vars_bn[2], self.vars_bn[3]
115 x &＃61; F.batch_norm(x, running_mean, running_var, weight&＃61;weight, bias&＃61;bias, training&＃61;bn_training)
116 x &＃61; F.relu(x) # 第2个relu
117 x &＃61; F.max_pool2d(x, kernel_size&＃61;2) # 第2个MAX_POOL层
118 weight, bias &＃61; params[8], params[9] # 第3个CONV层
119 x &＃61; F.conv2d(x, weight, bias, stride&＃61;1, padding&＃61;1)
120 weight, bias &＃61; params[10], params[11] # 第3个BN层
121 running_mean, running_var &＃61; self.vars_bn[4], self.vars_bn[5]
122 x &＃61; F.batch_norm(x, running_mean, running_var, weight&＃61;weight, bias&＃61;bias, training&＃61;bn_training)
123 x &＃61; F.relu(x) # 第3个relu
124 x &＃61; F.max_pool2d(x, kernel_size&＃61;2) # 第3个MAX_POOL层
125 weight, bias &＃61; params[12], params[13] # 第4个CONV层
126 x &＃61; F.conv2d(x, weight, bias, stride&＃61;1, padding&＃61;1)
127 weight, bias &＃61; params[14], params[15] # 第4个BN层
128 running_mean, running_var &＃61; self.vars_bn[6], self.vars_bn[7]
129 x &＃61; F.batch_norm(x, running_mean, running_var, weight&＃61;weight, bias&＃61;bias, training&＃61;bn_training)
130 x &＃61; F.relu(x) # 第4个relu
131 x &＃61; F.max_pool2d(x, kernel_size&＃61;2) # 第4个MAX_POOL层
132 x &＃61; paddle.reshape(x, [x.shape[0], -1]) ## flatten
133 weight, bias &＃61; params[-2], params[-1] # linear
134 x &＃61; F.linear(x, weight, bias)
135 output &＃61; x
136 return output
137
138 def parameters(self, include_sublayers&＃61;True):
139 return self.vars
元学习器类的代码如下&＃xff1a;
1class MetaLearner(nn.Layer):
2 def __init__(self, n_way, glob_update_step, glob_update_step_test, glob_meta_lr, glob_base_lr):
3 super(MetaLearner, self).__init__()
4 self.update_step &＃61; glob_update_step # task-level inner update steps
5 self.update_step_test &＃61; glob_update_step_test
6 self.net &＃61; MAML(n_way&＃61;n_way)
7 self.meta_lr &＃61; glob_meta_lr # 外循环学习率
8 self.base_lr &＃61; glob_base_lr # 内循环学习率
9 self.meta_optim &＃61; paddle.optimizer.Adam(learning_rate&＃61;self.meta_lr, parameters&＃61;self.net.parameters())
10
11 def forward(self, x_spt, y_spt, x_qry, y_qry):
12 task_num &＃61; x_spt.shape[0]
13 query_size &＃61; x_qry.shape[1] # 75 &＃61; 15 * 5
14 loss_list_qry &＃61; [0 for _ in range(self.update_step &＃43; 1)]
15 correct_list &＃61; [0 for _ in range(self.update_step &＃43; 1)]
16
17 # 内循环梯度手动更新&＃xff0c;外循环梯度使用定义好的更新器更新
18 for i in range(task_num):
19 # 第0步更新
20 y_hat &＃61; self.net(x_spt[i], params&＃61;None, bn_training&＃61;True) # (setsz, ways)
21 loss &＃61; F.cross_entropy(y_hat, y_spt[i])
22 grad &＃61; paddle.grad(loss, self.net.parameters()) # 计算所有loss相对于参数的梯度和
23 tuples &＃61; zip(grad, self.net.parameters()) # 将梯度和参数一一对应起来
24 # fast_weights这一步相当于求了一个\\theta - \\alpha*\\nabla(L)
25 fast_weights &＃61; list(map(lambda p: p[1] - self.base_lr * p[0], tuples))
26 # 在query集上测试&＃xff0c;计算准确率
27 # 这一步使用更新前的数据&＃xff0c;loss填入loss_list_qry[0]&＃xff0c;预测正确数填入correct_list[0]
28 with paddle.no_grad():
29 y_hat &＃61; self.net(x_qry[i], self.net.parameters(), bn_training&＃61;True)
30 loss_qry &＃61; F.cross_entropy(y_hat, y_qry[i])
31 loss_list_qry[0] &＃43;&＃61; loss_qry
32 pred_qry &＃61; F.softmax(y_hat, axis&＃61;1).argmax(axis&＃61;1) # size &＃61; (75) # axis取-1也行
33 correct &＃61; paddle.equal(pred_qry, y_qry[i]).numpy().sum().item()
34 correct_list[0] &＃43;&＃61; correct
35 # 使用更新后的数据在query集上测试。loss填入loss_list_qry[1]&＃xff0c;预测正确数填入correct_list[1]
36 with paddle.no_grad():
37 y_hat &＃61; self.net(x_qry[i], fast_weights, bn_training&＃61;True)
38 loss_qry &＃61; F.cross_entropy(y_hat, y_qry[i])
39 loss_list_qry[1] &＃43;&＃61; loss_qry
40 pred_qry &＃61; F.softmax(y_hat, axis&＃61;1).argmax(axis&＃61;1) # size &＃61; (75)
41 correct &＃61; paddle.equal(pred_qry, y_qry[i]).numpy().sum().item()
42 correct_list[1] &＃43;&＃61; correct
43
44 # 剩余更新步数
45 for k in range(1, self.update_step):
46 y_hat &＃61; self.net(x_spt[i], params&＃61;fast_weights, bn_training&＃61;True)
47 loss &＃61; F.cross_entropy(y_hat, y_spt[i])
48 grad &＃61; paddle.grad(loss, fast_weights)
49 tuples &＃61; zip(grad, fast_weights)
50 fast_weights &＃61; list(map(lambda p: p[1] - self.base_lr * p[0], tuples))
51
52 if k < self.update_step - 1:
53 with paddle.no_grad():
54 y_hat &＃61; self.net(x_qry[i], params&＃61;fast_weights, bn_training&＃61;True)
55 loss_qry &＃61; F.cross_entropy(y_hat, y_qry[i])
56 loss_list_qry[k &＃43; 1] &＃43;&＃61; loss_qry
57 else: # 对于最后一步update&＃xff0c;要记录loss计算的梯度值&＃xff0c;便于外循环的梯度传播
58 y_hat &＃61; self.net(x_qry[i], params&＃61;fast_weights, bn_training&＃61;True)
59 loss_qry &＃61; F.cross_entropy(y_hat, y_qry[i])
60 loss_list_qry[k &＃43; 1] &＃43;&＃61; loss_qry
61
62 with paddle.no_grad():
63 pred_qry &＃61; F.softmax(y_hat, axis&＃61;1).argmax(axis&＃61;1)
64 correct &＃61; paddle.equal(pred_qry, y_qry[i]).numpy().sum().item()
65 correct_list[k &＃43; 1] &＃43;&＃61; correct
66
67 loss_qry &＃61; loss_list_qry[-1] / task_num # 计算最后一次loss的平均值
68 self.meta_optim.clear_grad() # 梯度清零
69 loss_qry.backward()
70 self.meta_optim.step()
71
72 accs &＃61; np.array(correct_list) / (query_size * task_num) # 计算各更新步数acc的平均值
73 loss &＃61; np.array(loss_list_qry) / task_num # 计算各更新步数loss的平均值
74 return accs, loss
75
76 def finetunning(self, x_spt, y_spt, x_qry, y_qry):
77 # assert len(x_spt.shape) &＃61;&＃61; 4
78 query_size &＃61; x_qry.shape[0]
79 correct_list &＃61; [0 for _ in range(self.update_step_test &＃43; 1)]
80
81 new_net &＃61; deepcopy(self.net)
82 y_hat &＃61; new_net(x_spt)
83 loss &＃61; F.cross_entropy(y_hat, y_spt)
84 grad &＃61; paddle.grad(loss, new_net.parameters())
85 fast_weights &＃61; list(map(lambda p: p[1] - self.base_lr * p[0], zip(grad, new_net.parameters())))
86
87 # 在query集上测试&＃xff0c;计算准确率
88 # 这一步使用更新前的数据
89 with paddle.no_grad():
90 y_hat &＃61; new_net(x_qry, params&＃61;new_net.parameters(), bn_training&＃61;True)
91 pred_qry &＃61; F.softmax(y_hat, axis&＃61;1).argmax(axis&＃61;1) # size &＃61; (75)
92 correct &＃61; paddle.equal(pred_qry, y_qry).numpy().sum().item()
93 correct_list[0] &＃43;&＃61; correct
94
95 # 使用更新后的数据在query集上测试。
96 with paddle.no_grad():
97 y_hat &＃61; new_net(x_qry, params&＃61;fast_weights, bn_training&＃61;True)
98 pred_qry &＃61; F.softmax(y_hat, axis&＃61;1).argmax(axis&＃61;1) # size &＃61; (75)
99 correct &＃61; paddle.equal(pred_qry, y_qry).numpy().sum().item()
100 correct_list[1] &＃43;&＃61; correct
101
102 for k in range(1, self.update_step_test):
103 y_hat &＃61; new_net(x_spt, params&＃61;fast_weights, bn_training&＃61;True)
104 loss &＃61; F.cross_entropy(y_hat, y_spt)
105 grad &＃61; paddle.grad(loss, fast_weights)
106 fast_weights &＃61; list(map(lambda p: p[1] - self.base_lr * p[0], zip(grad, fast_weights)))
107
108 y_hat &＃61; new_net(x_qry, fast_weights, bn_training&＃61;True)
109
110 with paddle.no_grad():
111 pred_qry &＃61; F.softmax(y_hat, axis&＃61;1).argmax(axis&＃61;1)
112 correct &＃61; paddle.equal(pred_qry, y_qry).numpy().sum().item()
113 correct_list[k &＃43; 1] &＃43;&＃61; correct
114
115 del new_net
116 accs &＃61; np.array(correct_list) / query_size
117 return accs
复现结果
本项目在Omniglot数据集上进行了实验复现&＃xff0c;其复现的结果如下表所示&＃xff1a;
小结
本文对小样本学习领域的研究背景、基本概念、常用数据集进行了简要介绍&＃xff0c;重点阐述了MAML元学习模型的实现方法、实验结果和关键代码。该模型是入门小样本学习的必经之路&＃xff0c;也是评估新算法性能指标的基石。熟悉并掌握该经典模型&＃xff0c;将对今后的理论研究或实践应用奠定基础。飞桨官方的小样本学习工具包PaddleFSL已经包含了包括计算机视觉和自然语言处理应用问题的小样本学习解决方案&＃xff0c;如MAML&＃xff0c;ProtoNet&＃xff0c;Relation Net等等&＃xff0c;是首个基于飞桨的小样本学习工具包&＃xff0c;欢迎大家关注并一起探讨。
https://github.com/tata1661/FSL-Mate/tree/master/PaddleFSL
参考文献
[1] Vinyals O, Blundell C, Lillicrap T, et al. Matching Networks for One Shot Learning[J], 2016.
[2] Ravi S, Larochelle H. Optimization as a model for few-shot learning[J], 2016.
[3] Ren M, Triantafillou E, Ravi S, et al. Meta-learning for semi-supervised few-shot classification[J]. arXiv preprint arXiv:1803.00676, 2018.
[4] Oreshkin B N, Rodriguez P, Lacoste A. Tadam: Task dependent adaptive metric for improved few-shot learning[J]. arXiv preprint arXiv:1805.10123, 2018.
[5] Lake B, Salakhutdinov R, Gross J, et al. One shot learning of simple visual concepts[C]. Proceedings of the annual meeting of the cognitive science society, 2011.
[6] Wah C, Branson S, Welinder P, et al. The caltech-ucsd birds-200-2011 dataset[J], 2011.
[7] Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[C]. International Conference on Machine Learning, 2017: 1126-1135.
相关阅读
详解Swin Transformer核心实现&＃xff0c;经典模型也能快速调优
基于飞桨实现的“太空保卫战士”——地球同步静止轨道空间目标检测系统
关注【飞桨PaddlePaddle】公众号
获取更多技术内容~
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有